Re: Factor

After revisiting FizzBuzz yesterday to discuss a Lazy FizzBuzz using infinite lazy lists, I thought I would not return to the subject for awhile. Apparently, I was wrong!

Susam Pal just wrote a really fun article about Solving Fizz Buzz with Cosines:

We define a set of four functions { s0, s1, s2, s3 } for integers n by:

s0(n) = n

s1(n) = Fizz

s2(n) = Buzz

s3(n) = FizzBuzz

And from that, they derive a formula which is essentially a finite Fourier series for computing the nth value in the FizzBuzz sequence, showing a nice fixed periodic cycling across n mod 15, resolving at each value of n to either the integers 0, 1, 2, 3:

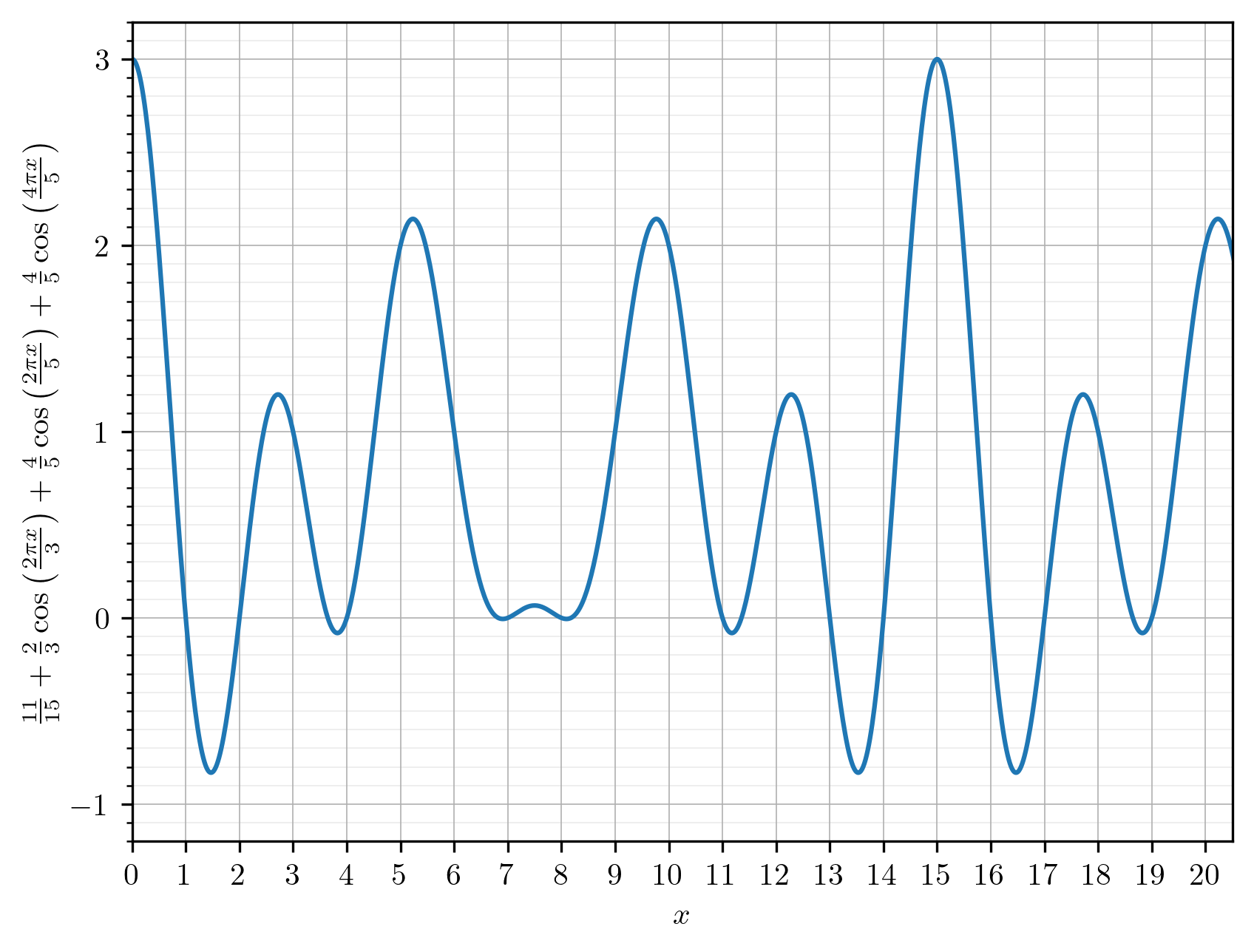
I recommend reading the whole article, but I will jump to an implementation of the formula in Factor:

:: fizzbuzz ( n -- val )
    11/15
    2/3 n * pi * cos 2/3 * +
    2/5 n * pi * cos 4/5 * +
    4/5 n * pi * cos + round >integer
    { n "Fizz" "Buzz" "FizzBuzz" } nth ;

And we can use that to compute the first few values in the sequence:

IN: scratchpad 1 ..= 100 [ fizzbuzz . ] each
1
2
"Fizz"
4
"Buzz"
"Fizz"
7
8
"Fizz"
"Buzz"
11
"Fizz"
13
14
"FizzBuzz"
16
17
"Fizz"
19
"Buzz"
...

Or, even some arbitrary values in the sequence:

IN: scratchpad 67 fizzbuzz .
67

IN: scratchpad 9,999,999 fizzbuzz .
"Fizz"

IN: scratchpad 10,000,000 fizzbuzz .
"Buzz"

IN: scratchpad 1,234,567,890 fizzbuzz .
"FizzBuzz"

Thats even more fun than using lazy lists!