Re: Factor

Admittedly, I struggle sometimes when I read the word “monoid”. It seems to always remind me of that saying “A Monad is just a Monoid in the Category of Endofunctors” which is both a tongue-twister, requires repeated effort to understand, and is sometimes used in casual conversation when jealously describing the features and capabilities of the Haskell programming language.

In any event, the topic of monoids came up recently on the Factor Discord server. Slava Pestov, the original creator of the Factor programming language, was describing recent work he was doing on some fun mathematical problems:

I’m searching for examples of finitely-presented monoids that cannot be presented by finite complete rewriting systems:

• ⟨a, b | aba=aa, baa=aab⟩ – my first result in this space.
• ⟨a, b | bab=aaa, bbb=bb⟩ – explore the equivalence class of a⁸ in this remarkable monoid.

He clarified in the discussion that “the Knuth-Bendix algorithm can solve many cases but not these two, which is how I found them in the first place”.

The second link above – made extra fun because it uses a=🍎 and b=🍌 to make a more emojiful experience – describes this specific problem in more detail and presents it as a simple game to play. You can see the available rules, the current state, and the next possible states achieved by applying either of the rules, which are bi-directional.

Your pie recipe calls for 10 apples, but you only have 8 apples.

Can you turn your 8 apples into 10 apples with these two magic spells?

• 🍌🍎🍌 ↔️ 🍎🍎🍎
• 🍌🍌🍌 ↔️ 🍌🍌

Current state:

🍎🍎🍎🍎🍎🍎🍎🍎

Tap to cast a spell:

1. 🍌🍎🍌🍎🍎🍎🍎🍎
2. 🍎🍌🍎🍌🍎🍎🍎🍎
3. 🍎🍎🍌🍎🍌🍎🍎🍎
4. 🍎🍎🍎🍌🍎🍌🍎🍎
5. 🍎🍎🍎🍎🍌🍎🍌🍎
6. 🍎🍎🍎🍎🍎🍌🍎🍌

When exploring things like this, many questions come to mind. For example:

1. Is this even solvable?
2. What is the shortest solution?
3. How many short solutions exist?
4. How many of the possible states lead to the solution?
5. How large is the set of all possible states?

After the link was shared, I must have clicked through about 5000 different state transitions hoping to randomly stumble upon the solution. And, eventually, recognized that it might be a good idea – or even possibly poetic – to do that exploration using Factor.

Warning: Spoilers ahead!

Let’s start by writing the rules:

CONSTANT: rules {
    { "bab" "aaa" }
    { "bbb" "bb" }
}

For convenience, we will make a sequence containing all the rules – since these are bi-directional and can be applied in either direction – using a literal expression.

CONSTANT: all-rules $[
    rules dup [ swap ] assoc-map append
]

We can make a word that takes a from node and applies a quotation to the result of rules a -> b. Notice that we’re able to use our previous work on finding subsequences:

:: each-move ( from a b quot: ( next -- ) -- )
    from dup a subseq-indices [
        cut a length tail b glue quot call
    ] with each ; inline

And then a word that returns all the next states:

: all-moves ( from -- moves )
    [ all-rules [ first2 [ , ] each-move ] with each ] { } make ;

It’s often good practice to try each step out during development, so let’s do that and show the first six possible next states match the ones from the game:

IN: scratchpad "aaaaaaaa" all-moves .
{
    "babaaaaa"
    "ababaaaa"
    "aababaaa"
    "aaababaa"
    "aaaababa"
    "aaaaabab"
}

The next state is nice to have, but we’re generally going to be accumulating paths which are a series of states achieved by traversing the graph of all possible states:

:: all-paths% ( path -- )
    path last all-rules [
        first2 [ path swap suffix , ] each-move
    ] with each ;

: all-paths ( paths -- paths' )
    [ [ all-paths% ] each ] { } make members ;

So, these are the first two steps in traversing the graph. You can see that some of the possible second moves end up circling back to the starting position, which makes sense since the rules are bi-directional and if applied can be un-applied on the next step.

IN: scratchpad { { "aaaaaaaa" } } all-paths dup . nl all-paths .
{
    { "aaaaaaaa" "babaaaaa" }
    { "aaaaaaaa" "ababaaaa" }
    { "aaaaaaaa" "aababaaa" }
    { "aaaaaaaa" "aaababaa" }
    { "aaaaaaaa" "aaaababa" }
    { "aaaaaaaa" "aaaaabab" }
}

{
    { "aaaaaaaa" "babaaaaa" "aaaaaaaa" }
    { "aaaaaaaa" "babaaaaa" "babbabaa" }
    { "aaaaaaaa" "babaaaaa" "babababa" }
    { "aaaaaaaa" "babaaaaa" "babaabab" }
    { "aaaaaaaa" "ababaaaa" "aaaaaaaa" }
    { "aaaaaaaa" "ababaaaa" "ababbaba" }
    { "aaaaaaaa" "ababaaaa" "abababab" }
    { "aaaaaaaa" "aababaaa" "aaaaaaaa" }
    { "aaaaaaaa" "aababaaa" "aababbab" }
    { "aaaaaaaa" "aaababaa" "aaaaaaaa" }
    { "aaaaaaaa" "aaababaa" "babbabaa" }
    { "aaaaaaaa" "aaaababa" "aaaaaaaa" }
    { "aaaaaaaa" "aaaababa" "babababa" }
    { "aaaaaaaa" "aaaababa" "ababbaba" }
    { "aaaaaaaa" "aaaaabab" "aaaaaaaa" }
    { "aaaaaaaa" "aaaaabab" "babaabab" }
    { "aaaaaaaa" "aaaaabab" "abababab" }
    { "aaaaaaaa" "aaaaabab" "aababbab" }
}

Let’s solve for the shortest paths, we keep track of states we’ve previously seen to avoid cycles, and we iterate using breadth-first-search until we find any solutions:

:: shortest-paths ( from to -- moves )
    HS{ from } clone :> seen
    { { from } }     :> stack!

    f [
        drop

        ! find all next possibilities
        stack all-paths

        ! reject ones that circle back to visited nodes
        [ last seen in? ] reject

        ! reject any that are over the length of ``to``
        to length '[ last length _ > ] reject stack!

        ! add the newly visited nodes
        stack [ last seen adjoin ] each

        ! stop when we find any solutions
        stack [ last to = ] filter dup empty?
    ] loop ;

Note: we reject any states that are longer than our goal state. This provides a nice way to cull the graph and make the search performance more reasonable. You could also choose not do that, and exhaustively search into that area. However, while this is not generally a valid approach to solving these types of problems, it is specifically a valid approach to this one.

There are quite a few shortest paths:

IN: scratchpad "aaaaaaaa" "aaaaaaaaaa" shortest-paths length .
560

Each of those contain 16 nodes, which means 15 rules were applied:

IN: scratchpad "aaaaaaaa" "aaaaaaaaaa" shortest-paths first length .
16

But they only go through a seemingly small number of nodes:

IN: scratchpad "aaaaaaaa" "aaaaaaaaaa" shortest-paths concat members length .
43

How many nodes are there in total in the graph? Let’s find out!

:: full-graph ( from to -- seen )
    HS{ from } clone :> seen

    { { from } } [
        ! find all next possibilities
        all-paths

        ! reject any that are over the length of ``to``
        to length '[ last length _ > ] reject

        ! only include ones that visit new nodes
        [ last seen ?adjoin ] filter
    ] until-empty seen ;

We can see that the shortest solutions go through about 15% of the nodes:

IN: scratchpad "aaaaaaaa" "aaaaaaaaaa" full-graph cardinality .
279

We can use our graph traversal approach and Graphviz to visualize where solutions are found, showing how some areas of the graph are quite hard to randomly get out of and then on the correct path to a solution. We draw the starting node green, the ending node blue, and the nodes that involved in the shortest path as gray:

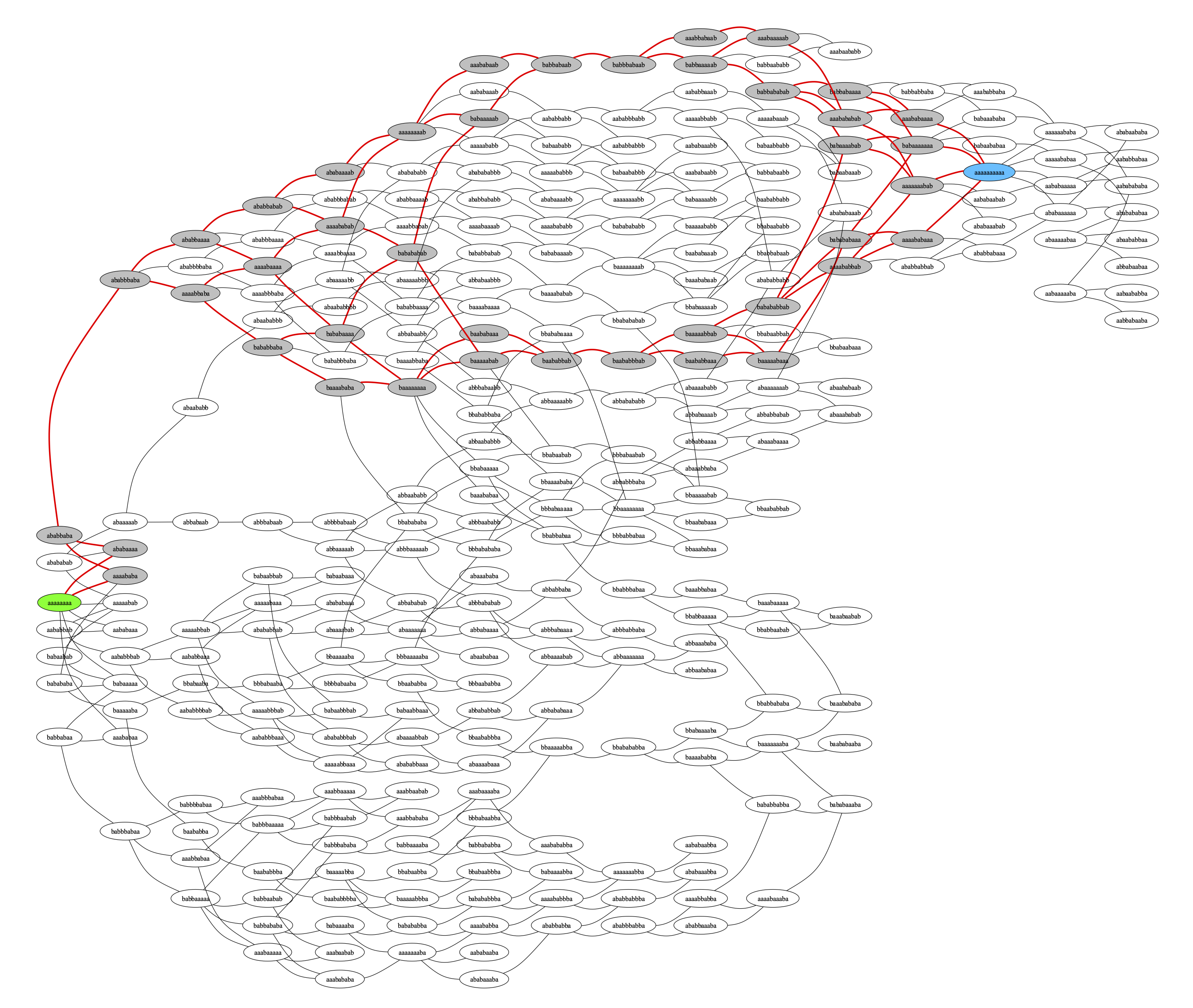
And that’s kind of interesting, but if we cluster nodes by their depth when first discovered, some other patterns show up:

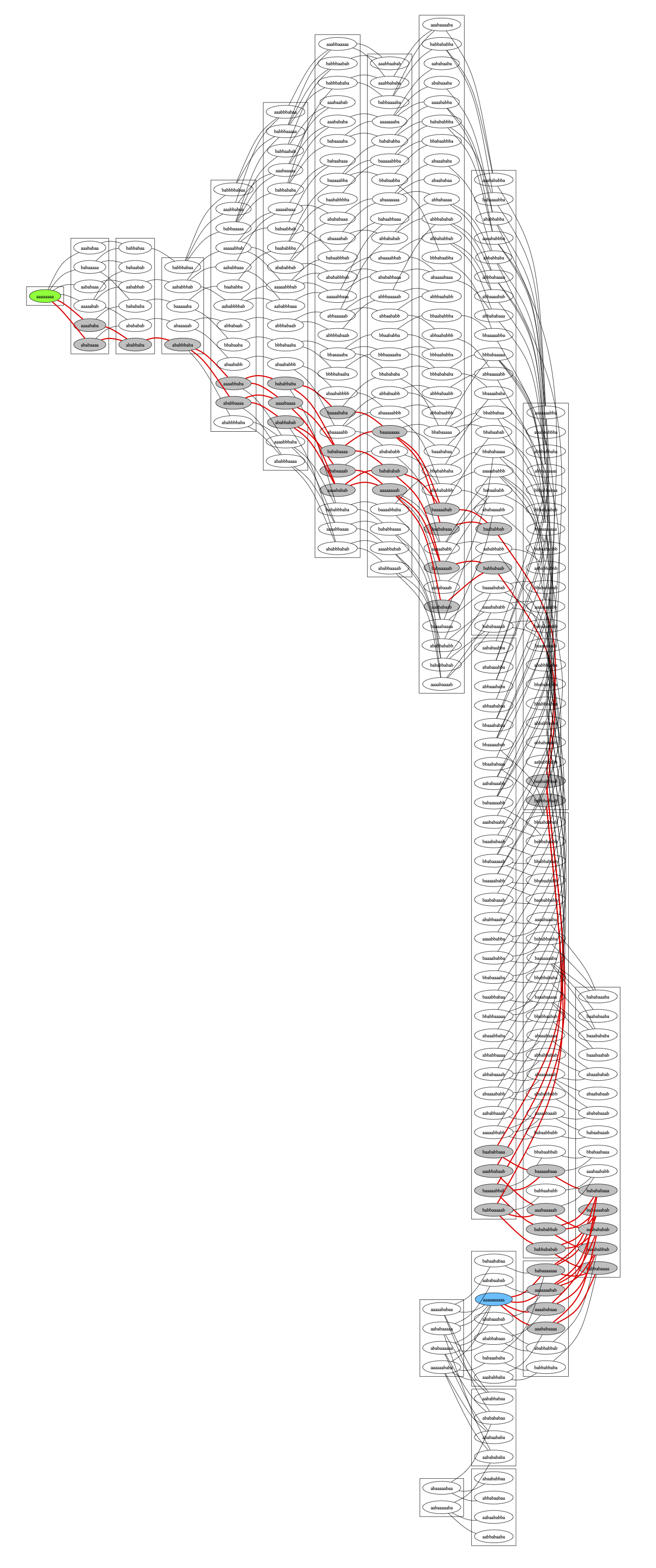
Such a fun problem!