Re: Factor

I have lately been curious about the Zig Programming Language and how it might be useful to Factor. In the process of doing some research, I bumped into a blog post about Converting decimal odds to probabilities with Zig, which shares some Zig source code for calculating sports betting odds:

As sports betting expands across the world, more and more players don’t understand tha math behind it. So, the purpose of this article it’s to clarify how to convert from decimal odds to the probability behind them. The calculations are implemented in Zig, a system programming language perfect to create CLI tools because it’s fast and simple.

It is particularly interesting given the growth and popularity of both sports betting on platforms like DraftKings, but also prediction markets like Polymarket and Manifold. You can read about some background information in Sports Betting Odds: How They Work and How To Read Them.

Note: I am not encouraging gambling, and in addition you should do your own research on the various platforms as there can be controversy about potential manipulation and transparency of the markets.

I don’t know much about (and do not do any) sports betting, but I thought it would be fun to learn about and then to translate some of these concepts to Factor.

Decimal

The “decimal odds” are popular in Europe and are the total returns including each original $1 bet if you win. These “decimal odds” effectively represent inverse probabilities. That is, if the odds are 4.5, then the probability is about 22% (which is 1/4.5).

Note: a variant of this is “fractional odds” popular in Britain which might instead quote those odds as 7/2 or 7-2 and describe the amount won ($7) in addition to the original bet ($2).

We can convert decimal odds to probabilities:

: odds>probs ( m -- n ) recip 100 * ;

: probs>odds ( n -- m ) 100 / recip ;

Sometimes the odds are quoted based on different outcomes – for example, in many team games there are three outcomes: win, lose, or tie. These probabilities should sum to 1, and seem to be often quoted with the payout included (typically less than 100%). The example given in the original blogpost is this:

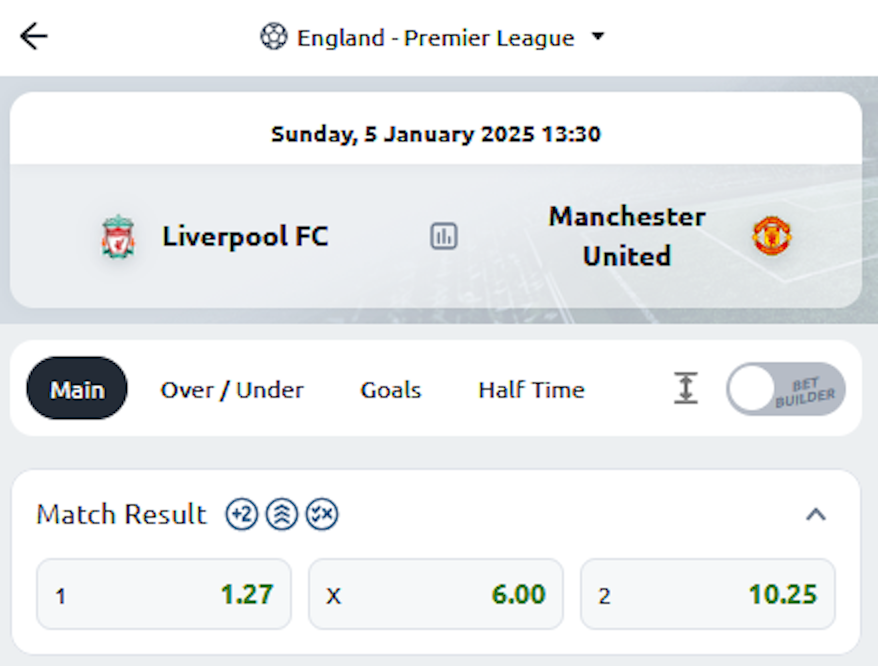
We can calculate the payout for a group of odds:

: compute-payout ( odds -- k )
    [ recip ] map-sum recip ;

And given the example from the blogpost, the payout is about 95%:

IN: scratchpad { 1.27 6.00 10.25 } compute-payout .
0.9509054938365546

Which means, you could convert odds to probabilities using this payout number:

: compute-probs ( odds -- probs )
    dup compute-payout '[ odds>probs _ * ] map ;

This shows the different probabilities of the outcomes, using printf to format the sequence:

IN: scratchpad { 1.27 6.0 10.25 } compute-probs "%[%.2f, %]" printf
{ 74.87, 15.85, 9.28 }

Moneyline

The “moneyline odds” are more popular in the United States. The original blogpost that I mention above did not go into details, but I was curious, so we will explore how moneyline payouts work. These are quoted as positive (underdogs) or negative (favorites) values, and are the amount you would need to bet to receive $100 of winnings.

Using the NFL example from the Investopedia article.

Let’s say a betting website (also known as an online sportsbook) priced an NFL game between the Pittsburgh Steelers and the Kansas City Chiefs with the following moneyline odds.

Steelers: +585

Chiefs: -760

We can convert moneyline odds to decimal odds:

: moneyline>odds ( moneyline -- odds )
    100 / dup 1 < [ recip neg ] when 1 + ;

: odds>moneyline ( odds -- moneyline )
    1 - dup 1 < [ recip neg ] when 100 * ;

And use that to calculate the implied relative probabilities of that game’s winner:

IN: scratchpad { 585 -760 } [ moneyline>odds ] map
               compute-probs "%[%.2f, %]" printf
{ 14.18, 85.82 }

Parlay

There are also “parlay odds” which are multiple bets linked together as one.

Let’s say you want to bet three heavy favorites on the moneyline because you’re confident each team will win, but not sure if they’ll cover the spread.

So you bet Packers -300 against the Lions, Patriots -200 vs. the Jets, and Eagles -150 at the Washington Commanders.

We can convert these to odds:

IN: scratchpad { -300 -200 -150 } [ moneyline>odds ] map .
{ 1+1/3 1+1/2 1+2/3 }

And write a word to convert it to a parlay outcome:

: compute-parlay ( moneyline -- parlay )
    [ moneyline>odds ] map product odds>moneyline ;

So, this example would have a parlay payout of 233:

IN: scratchpad { -300 -200 -150 } compute-parlay .
233+1/3

And a probability of 30%:

IN: scratchpad 233+1/3 moneyline>odds odds>probs .
30

There are probably aspects of this that I did not cover above, but it’s kinda fun to explore new topics that you don’t know much about and to learn!