Re: Factor

The Monte Carlo method is a method of estimation that uses random simulation to solve physical or mathematical problems. Named after the Monte Carlo Casino, you can think of the method as playing a game of chance many times and recording the outcomes (such as how frequently one wins or loses).

One classic example from the Wikipedia article is estimating the value of π (although there are many other ways to approximate the value of π):

For example, consider a circle inscribed in a unit square. Given that the circle and the square have a ratio of areas that is π/4, the value of π can be approximated using a Monte Carlo method:

1. Draw a square on the ground, then inscribe a circle within it.
2. Uniformly scatter some objects of uniform size (grains of rice or sand) over the square.
3. Count the number of objects inside the circle and the total number of objects.
4. The ratio of the two counts is an estimate of the ratio of the two areas, which is π/4. Multiply the result by 4 to estimate π.

You can visualize how this works by seeing the estimate get more correct as you increase the number of points:

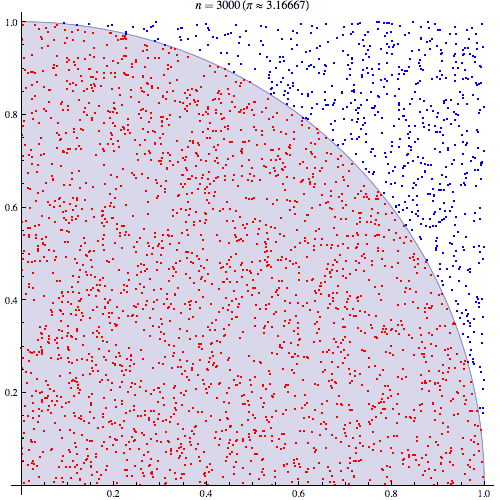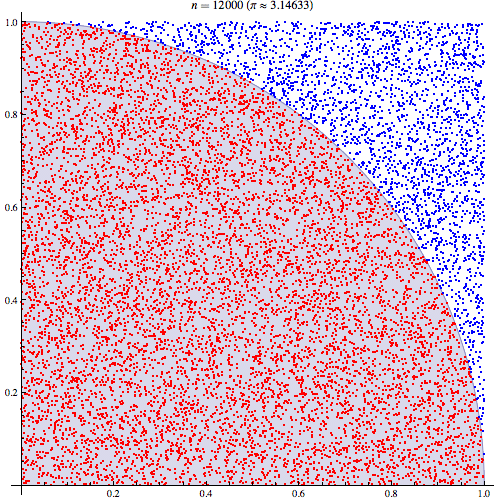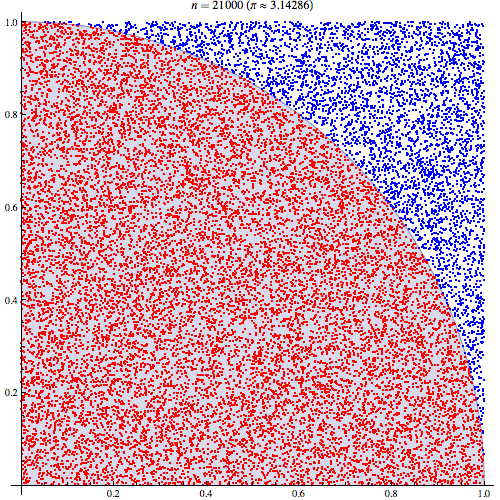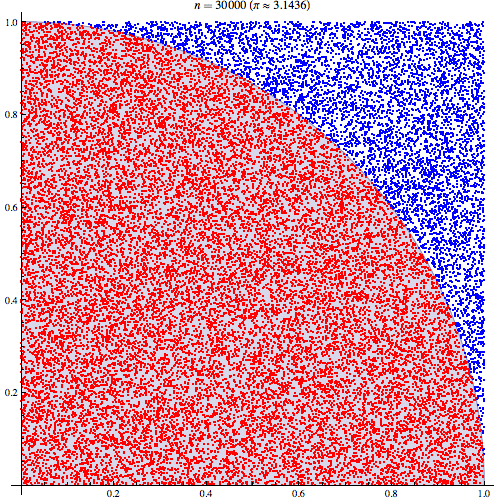
We can generate a random point inside the unit circle by generating two random-unit values:

: random-point ( -- x y )
    random-unit random-unit ;

Using the Pythagorean theorem, we can calculate the distance from the zero point. If the distance is less than or equal to 1.0, then it is inside the circle:

: inside-circle? ( x y -- ? )
    [ sq ] bi@ + sqrt 1.0 <= ;

We can then estimate the value of π by computing a number of points, taking the percentage that are inside the circle and multiplying by 4:

: estimate-pi ( points -- pi-estimate )
    0 swap [
        [ random-point inside-circle? [ 1 + ] when ] times
    ] keep /f 4 * ;

We can run this for varying numbers of points and see how it gets more accurate:

IN: scratchpad { 100 1,000 10,000 100,000 1,000,000 10,000,000 }
               [ estimate-pi . ] each
3.2
3.168
3.162
3.15176
3.14288
3.1418212