Powers of 2

Saturday, April 2, 2011

I came across a blog post discussing an interview question for developers:

“Write a function to determine if a number is a power of 2.”

Subsequently, I noticed a great discussion on StackOverflow discussing methods of solving this problem, and another blog post describing ten ways to do this in C. I’ve translated a few implementations into Factor to contrast the various approaches. The signature of the words we will create looks like this:

: power-of-2? ( n -- ? )

And some basic test cases used to verify that it works:

{ t } [ {  1 2 4 1024 } [ power-of-2? ] all? ] unit-test
{ f } [ { -1 0 3 1025 } [ power-of-2? ] any? ] unit-test

Implementations

We can shift the number to the right, checking to see that the first odd value observed is 1:

: shift-right/power-of-2? ( n -- ? )
    dup 0 <= [ drop f ] [ [ dup even? ] [ 2/ ] while 1 = ] if ;

Or, we can use a virtual sequence of bits and count the number of “on” bits (should be only 1):

: bits/power-of-2? ( n -- ? )
    dup 0 <= [ drop f ] [ make-bits [ t? ] count 1 = ] if ;

Or, we can compute the integer log2 raised to the second power, and compare:

: log2/power-of-2? ( n -- ? )
    dup 0 <= [ drop f ] [ dup log2 2^ = ] if ;

Or, we can calculate the next-power-of-2, and compare:

: next-power/power-of-2? ( n -- ? )
    dup 1 = [ drop t ] [ dup next-power-of-2 = ] if ;

Or, we can compare the number with its two’s complement:

: complement/power-of-2? ( n -- ? )
    dup 0 <= [ drop f ] [ dup dup neg bitand = ] if ;

Or, we can decrement the number and compare it with the original:

: decrement/power-of-2? ( n -- ? )
    dup 0 <= [ drop f ] [ dup 1 - bitand zero? ] if ;

Or, we can define a lookup table (using the literals vocabulary to define the table at compile time) holding all possible 64-bit powers of 2 (restricting the range of valid inputs to 64-bits):

CONSTANT: POWERS-OF-2 $[ 64 <iota> [ 2^ ] map ]

Using this, we can check a given number against all the values in the lookup table:

: check-all/power-of-2? ( n -- ? )
    POWERS-OF-2 member? ;

Or, we can do a linear search, stopping when we see numbers too large:

: linear-search/power-of-2? ( n -- ? )
    POWERS-OF-2 over [ >= ] curry find nip = ;

Or, knowing that the lookup table is sorted, we can do a binary search:

: binary-search/power-of-2? ( n -- ? )
    POWERS-OF-2 sorted-member? ;

Or, we can compute a hash-set (at compile time), and check for membership:

: hash-search/power-of-2? ( n -- ? )
    $[ POWERS-OF-2 fast-set ] in? ;

Or, we can use the integer log2 as an index into the lookup table.

: log-search/power-of-2? ( n -- ? )
    dup 0 <= [ drop f ] [ dup log2 POWERS-OF-2 nth = ] if ;

Testing

We can make a list of all our implementations:

CONSTANT: IMPLEMENTATIONS {
    shift-right/power-of-2?
    bits/power-of-2?
    log2/power-of-2?
    next-power/power-of-2?
    complement/power-of-2?
    decrement/power-of-2?
    check-all/power-of-2?
    linear-search/power-of-2?
    binary-search/power-of-2?
    hash-search/power-of-2?
    log-search/power-of-2?
}

And then test their functionality:

: test-power-of-2 ( -- ? )
    IMPLEMENTATIONS [
        1quotation [ call( n -- ? ) ] curry
        [ {  1 2 4 1024 } swap all? ]
        [ { -1 0 3 1025 } swap any? not ] bi and
    ] all? ;

Sure enough, they seem to work:

IN: scratchpad test-power-of-2 .
t

Performance

We can benchmark the performance of the various implementations operating on 1,000,000 random 32-bit numbers:

: bench-power-of-2 ( -- assoc )
    IMPLEMENTATIONS randomize 20 2^ [ random-32 ] replicate '[
        [ name>> "/" split1 drop ] [
            1quotation [ drop ] compose
            [ each ] curry [ _ ] prepose
            nano-count [ call( -- ) nano-count ] dip -
        ] bi
    ] { } map>assoc ;

Running the benchmark, we see that log2/power-of-2? is the (slightly) fastest version:

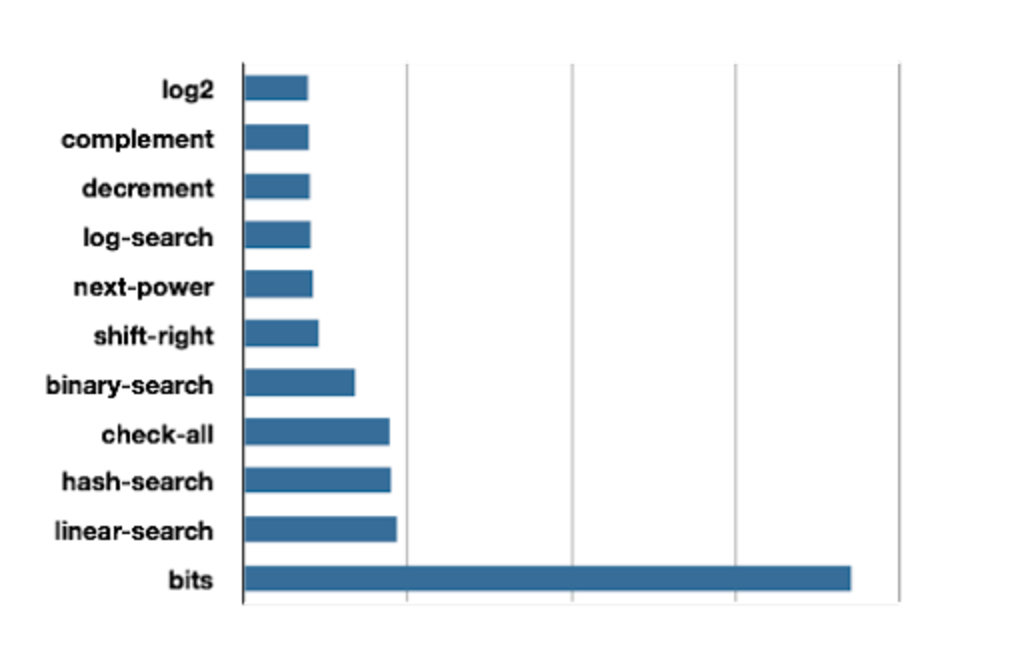
The raw numbers from one of my benchmark runs:

IN: scratchpad bench-power-of-2 sort-values .
{
    { "log2" 118107290 }
    { "complement" 119691428 }
    { "decrement" 121455742 }
    { "log-search" 122799186 }
    { "next-power" 127366447 }
    { "shift-right" 137695485 }
    { "binary-search" 204224141 }
    { "check-all" 267042396 }
    { "hash-search" 269629705 }
    { "linear-search" 280441186 }
    { "bits" 1112186059 }
}

Improvement

But, can we do better? We have already created a faster implementation than the math vocabulary, which defines power-of-2? using “decrement”. Focusing on that implementation, perhaps we can still introduce some improvements.

We can do less work, by exiting early using a short-circuit combinator if the first test fails:

: decrement+short/power-of-2? ( n -- ? )
    { [ dup 1 - bitand zero? ] [ 0 > ] } 1&& ;

Or, we can add type information, assuming only fixnum values (restricting our possible input values to a 60-bit number between -576,460,752,303,423,488 and 576,460,752,303,423,487):

TYPED: decrement+typed/power-of-2? ( n: fixnum -- ? )
    dup 0 <= [ drop f ] [ dup 1 - bitand zero? ] if ;

Or, if we are okay with restricting the input values, we can try writing it in C:

1. Build a simple C function in power-of-2.c:

#include <stdint.h>

int64_t isPowerOfTwo (int64_t x)
{
    return ((x > 0) && ((x & (x - 1)) == 0));
}

2. Build a C library we can use :

$ cc -fno-common -c power-of-2.c
$ cc -dynamiclib -install_name power-of-2.dylib \
     -o power-of-2.dylib power-of-2.o
$ sudo mv power-of-2.dylib /usr/local/lib

3. Wrap the C library from Factor (using the alien vocabulary):

USING: alien alien.c-types alien.syntax alien.libraries ;

"libpowerof2" "power-of-2.dylib" cdecl add-library

LIBRARY: libpowerof2

FUNCTION: int isPowerOfTwo ( int x )

4. And, finally, build a Factor word that uses it:

: decrement+alien/power-of-2? ( n -- ? )
    isPowerOfTwo 1 = ;

Running the benchmarks shows the typed version only slightly beating the short-circuit version, with a roughly 10% improvement:

{
    { "decrement+typed" 111711456 }
    { "decrement+short" 112070520 }
    { "decrement+alien" 113014058 }
    { "decrement" 123256748 }
}

Given that we want some ability to generalize our function to all integer inputs, I’d be happy declaring decrement+short/power-of-2? the “winner”. Can you do better?

The code for this is on my GitHub.