Re: Factor

Recently, I wanted a way to convert floating-point numbers into fractions using Factor. To do this (with any hope of being correct), I spent some time understanding how floating-point numbers are represented.

Two useful resources about floating-point numbers are an article entitled “What Every Computer Scientist Should Know About Floating-Point Arithmetic” and a website called The Floating-Point Guide.

Basic floating-point numbers are specified using a sign bit, an exponent, and a mantissa. Aside from some special numbers (e.g., +Inf, -Inf, NaN) and denormal numbers, the value of a floating-point can be calculated using the formula:

(-1)^sign × 2^{exponent\ -\ exponent\ bias} × 1.mantissa

We will be working with double precision floating point values (e.g., 64-bit values):

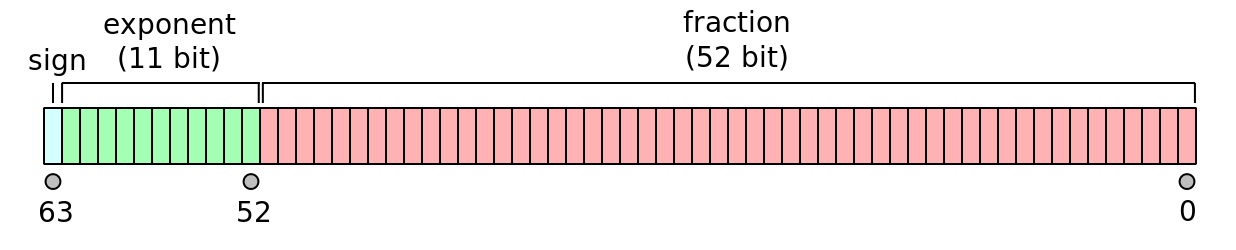
To extract the sign, exponent, and mantissa bits is fairly easy:

USING: kernel math math.bitwise math.functions ;

: sign ( bits -- sign )
    -63 shift ;

: exponent ( bits -- exponent )
    -52 shift 11 on-bits mask ;

: mantissa ( bits -- mantissa )
    52 on-bits mask ;

We are not going to support special values, so we throw an error if we encounter one:

: check-special ( n -- n )
    dup fp-special? [ "cannot be special" throw ] when ;

Converting to a ratio (e.g., numerator and denominator) is just a matter of computing the formula (with some special handling for denormal numbers where the exponent is zero):

: float>ratio ( n -- a/b )
    check-special double>bits
    [ sign zero? 1 -1 ? ] [ mantissa 52 2^ / ] [ exponent ] tri
    dup zero? [ 1 + ] [ [ 1 + ] dip ] if 1023 - 2 swap ^ * * ;

You can see this in action:

IN: scratchpad 0.5 float>ratio .
1/2

IN: scratchpad 12.5 float>ratio .
12+1/2

IN: scratchpad 0.333333333333333 float>ratio .
6004799503160655/18014398509481984

IN: scratchpad USE: math.constants
IN: scratchpad pi float>ratio .
3+39854788871587/281474976710656